S E P H ' S
[자료구조] 19. HashTable, HashMap(LinkedList / Red-Black-Tree) 본문
[자료구조] 19. HashTable, HashMap(LinkedList / Red-Black-Tree)
yoseph0310 2024. 1. 19. 19:50HashSet, LinkedHashSet과 같이 해시 개념을 접목한 자료구조들에 대해서 알아보고 해시충돌과 같은 개념 또한 살펴보았다.
이번 포스트에서는 HashTable, HashMap에 대해서 알아볼 것이다. 추가적으로 해시 충돌 포스트에서 이를 해결하기 위한 여러 방법들이 있었는데 이 또한 더 자세히 알아보도록 하자. 그리고 자료구조 파트의 포스트가 매우 많기 때문에 이쯤에서 한번 [Java] 4. Collection (List, Map, Set) 포스트에서 전체적인 자료구조 흐름을 짚고 넘어오면 좋을 것 같다.
HashTable, HashMap
두 자료구조 모두 공통된 특징을 갖고 있고 사용법도 유사하다. 둘 다 Map 인터페이스를 구현하고 있기 때문이다.
Key, Value 구조로 데이터를 저장하는 자료구조이고 빠르게 데이터를 검색할 수 있다. 각각의 Key 값에 해시함수를 통해 고유 index를 생성하고, 이 index를 활용하여 값을 저장하고 검색한다. 평균적으로 O(1)의 시간복잡도를 갖지만 연속적으로 검색해야하는 경우 O(n)까지 증가할 수 있다. 아래는 두 자료구조의 공통점과 차이점을 정리한 표이다.
| HashTable | HashMap | |
| 공통점 | 둘 다 Map Interface를 구현함 | |
| Thread-Safe | syncronized 키워드가 있어 동기화 진행 | syncronized 키워드가 없어 멀티스레드 환경에서 무결성을 보장하지 않음 |
| null 값 허용 | Key에 null 이 들어오면 NullPointerError 발생 | Key에 null이 들어오면 0으로 해싱하여 저장 |
| Enumeration 여부 | 제공 | 미제공 |
| 보조 해시 함수 | 미사용 | 사용. 성능상 이점이 있음 |
| API | Java 의 API. 컬렉션 프레임워크가 만들어지기 전에 존재하던 것으로 호환을 위해 남겨둔 것. | Java Collections Framework API |
위 표에 정리된 내용 중 몇가지를 풀어보자면, HashTable은 JDK 1.0 부터 있던 Java API이고 HashMap은 Java 2에서 처음 선보인 Java Collections FrameworkAPI에 속한 API이다. HashTable과 HashMap은 모두 Map Interface를 구현한 구현체이기 때문에 두 자료구조가 제공하는 기능은 같다.
다만 HashMap은 보조해시함수를 사용하므로 해시 충돌 가능성이 상대적으로 낮아 성능성 이점이 있다. HashTable의 현재 목적은 JRE 1.0, 1.1 환경을 대상으로 구현한 Java Application이 잘 동작하도록 하위 호환성을 제공하는 것에 있어 이 둘 사이의 성능, 기능을 비교하는 것은 큰 의미가 없다.
두 자료구조를 정의하자면, '키에 대한 해시값을 사용하여 값을 저장하고 조회하며, 키-값 쌍 개수에 따라 동적으로 크기가 증가하는 associate array(직역하자면 연관된 배열) 라고 할 수 있다. 이 associate array를 지칭하는 다른 용어가 있는데, 대표적으로 Map, Dictionary, Symbol Table 등이다.
해시 분포와 해시 충돌
동일하지 않은 객체 X, Y가 있을 때, (X.equals(Y) 가 false)일 때, X.hashCode() != Y.hashCode 이라면 이때 사용하는 해시 함수는 완전한 해시 함수라고 한다.
Boolean 같이 서로 구별되는 객체의 종류가 적거나, Integer, Long, Double 같은 Number 객체와 같은 경우 객체가 나타내려는 값 자체를 해시값으로 사용할 수 있기 때문에 완전한 해시 함수 대상으로 삼을 수 있다. 그러나 String이나 POJO(Plain Old Java Object)에 대해 완전 해시 함수를 제작하는 것은 사실상 불가능하다. 또한 적은 연산만으로 빠르게 동작할 수 있는 완전 해시 함수가 있다하더라도 그것을 HashMap 에서 사용할 수 있는 것은 아니다.
why?
HashMap은 기본적으로 각 객체의 hashCode() 메소드가 반환하는 값을 사용하는데 결과 자료형은 Int이다. 32비트 정수 자료형으로는 완전한 해시 함수를 만들 수 없다. 논리적으로 생성 가능한 객체 수가 2^32보다 많을 수 있기 때문이고, 모든 HashMap에서 O(1)을 보장하기 위해 랜덤 접근이 가능하게 하려면 크기가 2^32인 배열을 모든 HashMap이 가지고 있어야 하기 때문이다.
따라서 HashMap을 비롯한 많은 해시 함수를 이용하는 associate array 구현체에서는 메모리 절약을 위해 실제 해시 함수의 표현 정수 범위보다 작은 원소가 있는 배열만을 사용한다. 다음과 같이 객체에 대한 해시 코드의 나머지 값을 해시 버킷 인덱스 값으로 사용한다.
int index = X.hashCode() % M;
많이 보던놈이다.
이 방식을 사용하면 서로 다른 해시 코드를 가지는 서로 다른 객체가 1/M 확률로 같은 해시 버킷을 사용하게 된다. 이는 해시 함수가 얼마나 해시 충돌을 회피하도록 잘 구현되었느냐에 상관없이 발생할 수 있는 다른 종류의 해시 충돌이다.
// 만약 X, Y의 해시코드가 각각 101, 1이고 M이 100이면 다음과 같이 나오게 된다.
int X_hashCode = 101;
int Y_hashCode = 1;
// X_hashCode % M = 1;
// Y_hashCode % M = 1;
// 결과적으로 두 객체의 hash index가 같다.
이렇게 해시 충돌이 발생하더라도 키-값 쌍 데이터를 잘 저장하고 조회할 수 있게 하는 방식에는 대표적으로 Open Addressing, Separate Chaining 이 있다. 이 둘 이외에도 여러 방법이 있지만 모두 이 둘을 응용한 방식이다.
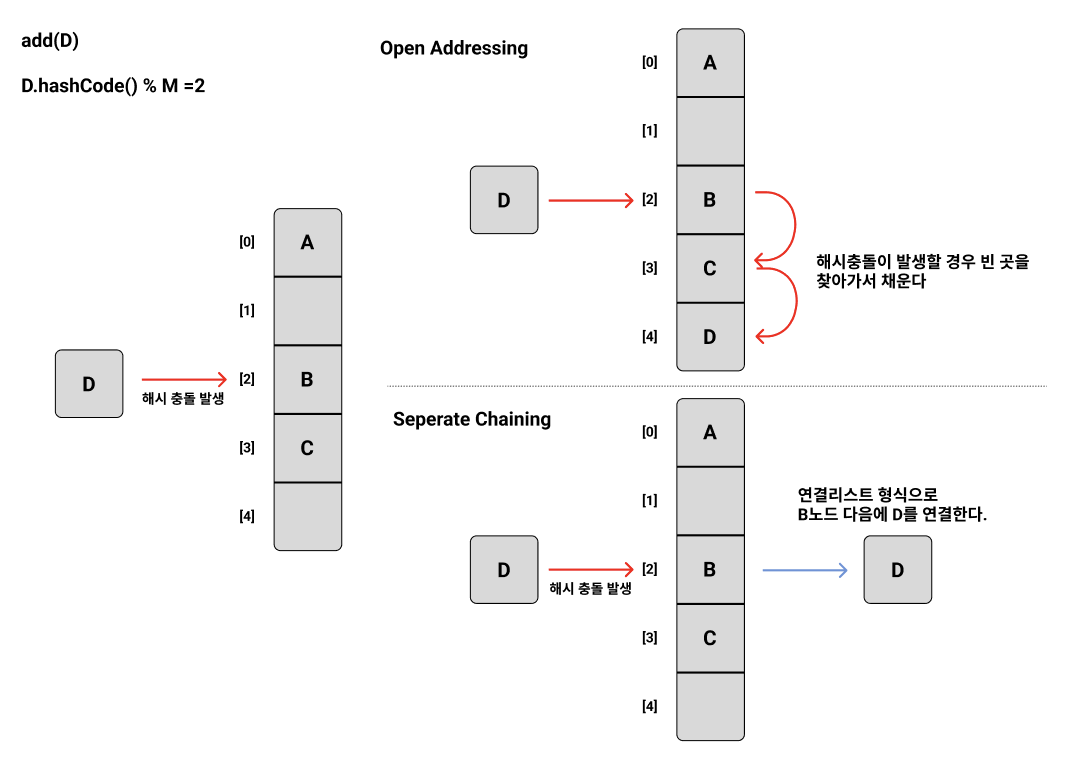
Open Addressing은 삽입하려는 해시 버킷이 이미 사용중이라면 다른 해시 버킷을 찾아 삽입하는 방식이다. 데이터를 저장/조회할 해시 버킷을 찾을 때에는 Linear Probing, Quadratic Probing 등의 방법을 사용한다.
- 선형 탐사 (Linear probing)
- 충돌이 발생했을 때 그 옆자리가 비어있는지 살펴보고, 비어있을 경우 그 자리에 대신 저장하는 방식. 위의 이미지가 선형 탐사의 그림이다.
- 계산이 단순하다는 장점이 있으나 검색에 많은 시간이 소요되며 테이블 내에 데이터들이 일정한 키 값으로 모이는 현상이 발생한다.
- 제곱 탐사 (Quadratic probing)
- 선형 조사법이 n 칸 옆을 검사한다면 제곱 탐사는 n^2 칸 옆을 검사하는 것이다.
- 일정한 키 값으로 모이는 현상은 방지하겠으나 모든 공간을 다 검사하지는 않게 된다.
- 이중 해싱 (Double hashing)
- 해시 함수를 이중으로 두어서 하나는 최초의 주소를 얻고 다른 하나는 충돌이 발생했을 때 빈칸을 찾을 인덱스를 얻기 위해 사용된다.
- 재해싱 (Rehashing)
- Hash Table의 크기를 늘리고 크기에 맞춰 테이블 내 모든 데이터를 다시 해싱하는 방법이다.
- 다시 재배치가 되는 것은 좋으나 상당히 많은 비용이 발생한다.
Separate Chaining에서 각 배열의 인자는 인덱스가 같은 해시 버킷을 연결한 링크드리스트의 첫 부분, 즉 Head이다.
두 방식 모두 Worst Case는 O(M)
Open Addressing
[장점]
- 해시 충돌이 일어날 가능성이 적기 때문에 데이터의 개수가 작을수록 속도가 빨라진다.
- 연속된 공간에 데이터를 저장하기 때문에 캐시 효율이 좋아진다.
[단점]
- 해시 충돌이 발생하면 해당 객체의 인덱스 값이 바뀐다.
- 부하율 (load factor) 즉, 테이블에 저장된 데이터가 많아질수록(= 밀도가 높아질수록) 성능이 급격히 저하된다. 배열의 크기가 커지면 L1, L2 캐시 적중률이 낮아지기 때문이다.
Separate Chaining
[장점]
- 해시 충돌이 일어나더라도 연결리스트로 노드가 연결되기에 index가 변하지 않는다.
- 테이블의 각 인덱스는 연결리스트로 구현되기 때문에 데이터 개수의 제약을 거의 받지 않는다.
[단점]
- 부하율 (load factor) 에 따라 선형적으로 성능이 저하된다.
- 부하율이 작을 경우에는 Open Addressing 방식이 더 빠르다.
Java HashMap에서 사용하는 방식은 Separate Chaining이다. Open Addressing은 데이터를 삭제할 때 처리가 효율적이지 않다. HashMap에서 remove() 메소드는 매우 빈번하게 호출될 수 있기 때문이다. 게다가 키-값 쌍 개수가 일정 개수 이상으로 많아지면 일반적으로 Open Addressing은 Separate Chaining보다 느리다. Open Addressing의 경우 해시 버킷을 채운 밀도가 높아질 수록 Worst Case 발생 빈도가 더욱 높아지기 때문이다. 반면 Separate Chaining의 경우 해시 충돌 발생 가능성을 조정할 수 있다면 Worst Case 또는 그에 가까운 일이 발생하는 것을 줄일 수 있다. 이것은 보조해시함수에 대한 내용을 다룰때 더 자세히 알아보자.
Java 8 HashMap 에서의 Separate Chaining
Java 2부터 7까지의 HashMap에서 Separate Chaining 구현 코드는 조금씩 다르지만, 구현 알고리즘 자체는 같았다. 만약 객체의 해시 함수 값이 균등 분포 상태라고 하면 get() 호출에 대한 기댓값은 N/M이다. 그러나 Java 8 에서는 더 나은 logN/M을 보장한다. 데이터의 개수가 많아지면, Separate Chaining에서 링크드 리스트 대신 트리를 사용하기 때문이다. 데이터의 개수가 많아지면 N/M과 logN/M의 차이는 무시할 수 없다. 게다가 실제 해시 값은 균등 분포가 아닐뿐더러 birthday problem이 설명하듯 일부 해시 버킷 몇개에 데이터가 집중될 수 있다. 그래서 데이터의 개수가 일정 이상일 경우 링크드 리스트 대신 트리를 사용하는 것이 성능상 이점이 있다.
링크드리스트냐, 트리냐에 대한 기준은 하나의 해시 버킷에 할당된 키-값 쌍의 개수이다. Java 8 HashMap 에서는 상수형태로 기준을 정하고 있다. 즉 하나의 해시 버킷에 8개의 키-값쌍이 모이면 링크드 리스트를 트리로 변경한다. 만약 해당 버킷의 데이터를 삭제하여 6개가 되면 다시 링크드 리스트로 변경한다. 트리는 링크드 리스트보다 메모리 사용량이 많고 데이터의 개수가 적을 때 트리와 링크드 리스트의 Worst Case 수행 시간 차이 비교는 의미가 없기 때문이다. 8과 6으로 2이상의 차이를 둔 이유는 만약 차이가 1이라면 어떤 한 키-값 쌍이 반복되어 삽입삭제되는 경우 불필요하게 트리와 링크드리스트를 변경하는 일이 반복되어 성능 저하가 발생할 수 있기 때문이다.
Birthday Problem
이 문제는 해시 충돌 가능성을 뒷받침하는 대표적 예시이다. 만약 여러 사람이 모였을 때, 생일이 겹치는 사람이 있을 확률은 매우 적을 것으로 예상하지만 실제로 23명만 모이더라도 그 확률은 50%가 넘어가며 상당히 높은 확률을 보인다.
static final int TREEIFY_THRESHOLD = 8;
static final int UNTREEIFY_THRESHOLD = 6;
Java 8 HashMap 에서는 Entry 클래스 대신 Node 클래스를 사용한다. Node 클래스 자체는 사실상 Java 7 의 Entry 클래스와 내용이 같지만, 링크드 리스트 대신 트리를 사용할 수 있도록 하위 클래스인 TreeNode가 있다는 것이 Java 7 HashMap과 다르다.
이때 사용하는 트리가 Red-Black-Tree 인데, Java Collections Framework의 TreeMap과 구현이 거의 같다. 트리 순회시 사용하는 대소 판단 기준은 해시 함수 값이다. 해시 값을 대소 판단 기준으로 사용하면 Total Ordering에 문제가 생기는데, Java 8 HashMap에서는 이를 tieBreakOrder() 메소드로 해결한다. Red-Black-Tree에 대해서는 다음 포스팅에서 더 다루도록 하겠다.
transient Node<K,V>[] table;
static class Node<K,V> implements Map.Entry<K,V> {
// 클래스 이름은 다르지만, Java 7의 Entry 클래스와 구현 내용은 같다.
}
// LinkedHashMap.Entry는 HashMap.Node를 상속한 클래스다.
// 따라서 TreeNode 객체를 table 배열에 저장할 수 있다.
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent;
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev;
// Red Black Tree에서 노드는 Red이거나 Black이다.
boolean red;
TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
final TreeNode<K,V> root() {
// Tree 노드의 root를 반환한다.
}
static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
// 해시 버킷에 트리를 저장할 때에는, root 노드에 가장 먼저 접근해야 한다.
}
// 순회하며 트리 노드 조회
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {}
final TreeNode<K,V> getTreeNode(int h, Object k) {}
static int tieBreakOrder(Object a, Object b) {
// TreeNode에서 어떤 두 키의comparator 값이 같다면 서로 동등하게 취급된다.
// 그런데 어떤 두 개의 키의 hash 값이 서로 같아도 이 둘은 서로 동등하지
// 않을 수 있다. 따라서 어떤 두 개의 키에 대한 해시 함수 값이 같을 경우,
// 임의로 대소 관계를 지정할 필요가 있는 경우가 있다.
}
final void treeify(Node<K,V>[] tab) {
// 링크드 리스트를 트리로 변환한다.
}
final Node<K,V> untreeify(HashMap<K,V> map) {
// 트리를 링크드 리스트로 변환한다.
}
// 다음 두 개 메서드의 역할은 메서드 이름만 읽어도 알 수 있다.
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {}
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
boolean movable) {}
// Red Black 구성 규칙에 따라 균형을 유지하기 위한 것이다.
final void split (…)
static <K,V> TreeNode<K,V> rotateLeft(…)
static <K,V> TreeNode<K,V> rotateRight(…)
static <K,V> TreeNode<K,V> balanceInsertion(…)
static <K,V> TreeNode<K,V> balanceDeletion(…)
static <K,V> boolean checkInvariants(TreeNode<K,V> t) {
// Tree가 규칙에 맞게 잘 생성된 것인지 판단하는 메서드다.
}
}
해시 버킷 동적 확장
해시 버킷의 개수가 적다면 메모리 사용을 아낄 수 있지만 해시 충돌로 인해 성능상 손실이 발생한다. 그래서 해시맵은 키-값 쌍 데이터 개수가 일정 개수 이상이 되면, 해시 버킷 수를 두배로 늘린다. 이렇게 해시 버킷 개수를 늘리면 N/M 값도 작아져 해시 충돌로 인한 성능 저하를 어느 정도 해결할 수 있다.
해시 버킷 개수의 기본 값은 16이고 데이터 개수가 임계점에 다다르면 해시 버킷 개수를 두배씩 증가시킨다. 버킷의 최대 개수는 2^30개이다. 그런데 이렇게 버킷 수가 두배 증가할 때마다 모든 키-값 데이터를 읽어 새로운 Separate Chaining을 구성해야 하는 문제가 있다. 해시맵 생성자의 인자로 초기 해시 버킷 개수를 지정할 수 있으므로 해당 해시맵 객체에 저장될 데이터의 개수가 어느 정도인지 예측 가능한 경우에는 이를 생성자의 인자로 지정하면 불필요한 Separate Chaining을 재구성하지 않을 수 있다.
// 인자로 사용하는 newCapacity는 언제나 2a이다.
void resize(int newCapacity) {
Entry[] oldTable = table;
int oldCapacity = oldTable.length;
// MAXIMIM_CAPACITY는 230이다.
if (oldCapacity == MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return;
}
Entry[] newTable = new Entry[newCapacity];
// 새 해시 버킷을 생성한 다음 기존의 모든 키-값 데이터들을
// 새 해시 버킷에 저장한다.
transfer(newTable, initHashSeedAsNeeded(newCapacity));
table = newTable;
threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
}
void transfer(Entry[] newTable, boolean rehash) {
int newCapacity = newTable.length;
// 모든 해시 버킷을 순회하면서
for (Entry<K,V> e : table) {
// 각 해시 버킷에 있는 링크드 리스트를 순회하면서
while(null != e) {
Entry<K,V> next = e.next;
if (rehash) {
e.hash = null == e.key ? 0 : hash(e.key);
}
// 해시 버킷 개수가 변경되었기 때문에
// index 값(hashCode % M)을 다시 계산해야 한다.
int i = indexFor(e.hash, newCapacity);
e.next = newTable[i];
newTable[i] = e;
e = next;
}
}
}
해시 버킷 크기를 두 배로 확장하는 임계점은 현재 데이터 개수가 load factor(부하율) * 현재 해시 버킷 개수에 이를 때이다. 이 load factor는 0.75 즉 3/4이다. 이 부하율 또한 HashMap 의 생성자에서 지정할 수 있다.
임계점에 이르면 항상 해시 버킷 크기를 두 배로 확장하기 때문에 N개의 데이터를 삽입했을 때의 키-값 쌍 접근 횟수는 다음과 같이 분석할 수 있다.
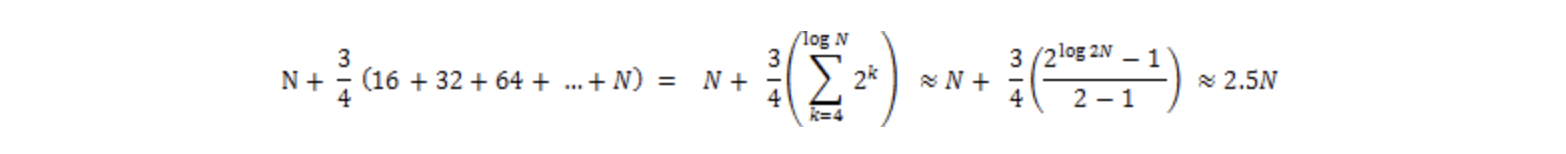
기본 생성자로 생성한 HashMap을 이용하여 많은 양의 데이터를 삽입할 때에는 최적의 해시 버킷 개수를 지정한 것보다 약 2.5배 많이 키값쌍 데이터에 접근해야 한다. 이는 곧 수행시간이 2.5배 길어진다고 할 수 있다. 따라서 성능을 높이기 위해서는 HashMap 객체를 생성할 때 적정한 해시 버킷 개수를 지정해야 한다.
그런데 이렇게 해시 버킷 크기를 두 배로 확장하는 것에는 결정적인 문제가 있다. 해시 버킷의 개수 M이 2^a 꼴이 되므로 index = X.hashCode() % M 을 계산할 때 X.hashCode()의 하위 a개의 비트만 사용하게 된다는 것이다. 즉 해시함수가 32비트 영역을 고르게 했더라도 해시 값을 2의 승수로 나누면 해시 충돌이 쉽게 발생할 수 있다는 것이다. 이 때문에 보조 해시 함수가 필요하다.
보조 해시 함수
index = X.hashCode() % M 을 계산할 때 사용하는 M 값은 소수일 때 index 값 분포가 가장 균등할 수 있다. 그러나 M 값이 소수가 아니기 때문에 별도의 보조 해시 함수를 이용하여 index 값 분포가 가급적 균등할 수 있도록 해야 한다.
보조 해시 함수의 목적은 '키'의 해시 값을 변형하여 해시 충돌 가능성을 줄이는 것이다. 이 보조 해시 함수는 JDK 1.4에 처음 등장했다. Java 5 ~ Java 7은 같은 방식의 보조 해시 함수를 사용하고, Java 8부터는 다시 새로운 방식의 보조 해시 함수를 사용하고 있다.
final int hash(Object k) {
// Java 7부터는 JRE를 실행할 때, 데이터 개수가 일정 이상이면
// String 객체에 대해서 JVM에서 제공하는 별도의 옵션으로
// 해시 함수를 사용하도록 할 수 있다.
// 만약 이 옵션을 사용하지 않으면 hashSeed의 값은 0이다.
int h = hashSeed;
if (0 != h && k instanceof String) {
return sun.misc.Hashing.stringHash32((String) k);
}
h ^= k.hashCode();
// 해시 버킷의 개수가 2a이기 때문에 해시 값의 a비트 값만을
// 해시 버킷의 인덱스로 사용한다. 따라서 상위 비트의 값이
// 해시 버킷의 인덱스 값을 결정할 때 반영될 수 있도록
// shift 연산과 XOR 연산을 사용하여, 원래의 해시 값이 a비트 내에서
// 최대한 값이 겹치지 않고 구별되게 한다.
h ^= (h >>> 20) ^ (h >>> 12);
return h ^ (h >>> 7) ^ (h >>> 4);
}(Java 7 HashMap 보조 해시 함수)
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}(Java 8 HashMap 보조 해시 함수)
Java 8 HashMap 보조 해시 함수는 상위 16 비트 값을 XOR 연산하는 매우 단순한 형태로 보조해시 함수를 사용한다. 이유로는 첫째, Java 8에서는 해시 충돌이 많으면 링크드 리스트 대신 트리를 사용하므로 해시 충돌 시 발생할 수 있는 성능 문제가 완화되었기 때문이고 둘째, 최근 해시 함수는 균등 분포가 잘 되게 만들어지는 경향이 많아 7까지 사용했던 보조 해시 함수의 효과가 크지 않기 때문이다. 두번째 이유가 더 결정적 원인이 되어 Java 8에서는 보조 해시 함수의 구현을 바꾸게 됐다.
개념상 해시 버킷 인덱스를 계산할 때는 index = X.hashCode % M처럼 나머지 연산을 사용하는 것이 맞으나, M 값이 2^a일때는 해시 함수의 하위 a 비트 만을 취한 것과 같다. 따라서 나머지 연산 대신 '1 << a - 1' 와 비트 논리곱 (AND, &)연산을 사용하면 수행이 훨씬 더 빠르다.
String 객체에 대한 해시 함수
String 객체에 대한 해시 함수 수행 시간은 문자열 길이에 비례한다.
때문에 JDK 1.1에서는 String 객체에 대해 빠른 해시 함수를 수행하기 위해 일정 간격의 문자에 대한 해시를 누적한 값을 문자열에 대한 해시 함수로 사용했다.
public int hashCode() {
int hash = 0;
int skip = Math.max(1, length() / 8);
for (int i = 0; i < length(): i+= skip)
hash = s[i] + (37 * hash);
return hash;
}
모든 문자에 대한 해시 함수를 계산하는 것이 아닌 문자열 길이가 16을 넘으면 최소 하나의 문자를 건너가며 해시 함수를 계산했다. 그러나 이런 방식은 심각한 문제를 야기한다. 웹상 URL은 길이가 수십 글자에 이르며 앞 부분은 동일하게 구성되는 경우가 많다. 이 경우 서로 다른 URL의 해시 값이 같아지는 빈도가 매우 높아질 수 있음을 알수 있다. 따라서 이 방식은 사용하지 않고 다음 예제에서 보는 방식을 계속 사용하고 있다.
public int hashCode() {
int h = hash;
if (h == 0 && value.length > 0) {
char val[] = value;
for (int i = 0; i < value.length; i++) {
h = 31 * h + val[i];
}
hash = h;
}
return h;
}
위 예제는 Horner's method를 구현한 것이다. 다항식을 계산하기 쉽도록 단항식으로 이루어진 식으로 표현하는 것이다. 위 예제에서 계산하고자 하는 해시 값 h는 다음과 같다.
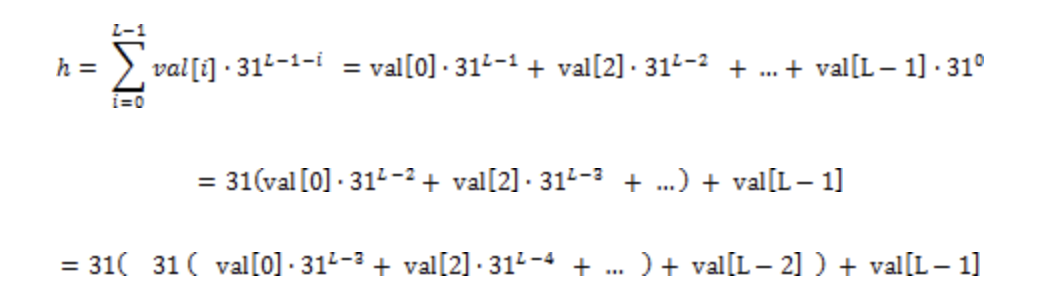
이렇게 단항식을 재귀적으로 사용하여 다항식 연산을 표현할 수 있다.
String 객체 해시 함수에서 31을 사용하는 이유는 31이 소수이며 또한 어떤 수에 31을 곱하는 것은 빠르게 계산할 수 있기 때문이다.
31N = 32N - N 인데, 32는 2^5이니 어떤 수에 대한 32를 곱한 값은 shift 연산으로 쉽게 구할 수 있다.
따라서 N에 31을 곱한 값은, (N << 5) - N 과 같다. 31을 곱하는 연산은 이렇게 최적화된 머신 코드로 생성할 수 있어 String 클래스에서 해시 값을 계산할 때는 31을 승수로 사용한다.
정리
Java HashMap 에서는 해시 충돌을 방지하기 위해 Seperate Chaining과 보조 해시 함수를 사용한다는 것, Java 8에서는 Seperate Chaining 에서 링크드리스트 대신 트리를 사용하기도 한다는 것, 그리고 String 클래스의 hashCode() 메소드에서 31을 승수로 사용하는 이유는 성능 형성 도모를 위한 것이라고 정리할 수 있다.
웹 애플리케이션 서버의 경우에는 HttpRequest가 생성될 때마다 여러 개의 HashMap이 생성된다. 수많은 HashMap 객체가 1초도 안되는 시간에 생성되고 GC(Garbage Collection)대상이 된다. 컴퓨터 메모리 크기가 보편적으로 증가하게 됨에 따라, 메모리 중심적인 애플리케이션 제작도 증가했다. 따라서 갈수록 해시맵에 더 많은 데이터를 저장하고 있다고 할 수 있다.
출처
https://d2.naver.com/helloworld/831311
'Programing & Coding > Data Structure' 카테고리의 다른 글
| [자료구조] 18. 트리(Tree)의 개념 (0) | 2023.07.19 |
|---|---|
| [자료구조] 17. Linked Hash Set (연결 해시 셋) (0) | 2023.07.19 |
| [자료구조] 16. 해시 충돌 (0) | 2023.07.17 |
| [자료구조] 15. HashSet (해시 셋) (1) | 2023.07.16 |
| [자료구조] 14. Java 셋 인터페이스 (Set Interface) (0) | 2023.07.13 |




